Test set: Accuracy: 9841/10000 (98%)
Classifying MNIST
DL Course
Instructor: Hasan A. Poonawala, Joseph Kershaw
Mechanical and Aerospace Engineering
University of Kentucky, Lexington, KY, USA
MNIST Dataset
- Goal: Zip-code recognition for mail sorting
- training images of digits -
- test images
- Smaller USPS dataset had train and test images
- Humans had a 2.5% error rate (source).
MNIST Samples

Each image is with grayscale value in
MNIST Samples
import torch ## See `./code/mnist/viz_mnist.py`
from torchvision import datasets, transforms
import matplotlib.pyplot as plt
import numpy as np
# 1. Data
transform = transforms.Compose([ ## transform the raw data from the file while loading
transforms.ToTensor(),
transforms.Normalize((0.1307,), (0.3081,)) ## mean, std image -> (image - mean)/std
])
train_dataset = datasets.MNIST('data', train=True, download=True, transform=transform)
random_array = np.random.randint(0, 59999, size=6)
fig, axes = plt.subplots(nrows=2, ncols=3, figsize=(10, 8))
axes = axes.flatten()
for i in range(6):
image, label = train_dataset[random_array[i]]
axes[i].imshow(image[0], cmap="gray")
axes[i].set_title(f"label: {label}")MNIST Classifier

MNIST Classifier
## See `./code/mnist/test_mnist.py`
import torch
from torchvision.datasets import MNIST
import torch
import torch.nn as nn
import torch.optim as optim
import torch.nn.functional as F
from torchvision import datasets, transforms
import matplotlib.pyplot as plt
# 1. Data
transform = transforms.Compose([
transforms.ToTensor(),
transforms.Lambda(lambda x: x.view(-1))
])
train_dataset = datasets.MNIST('data', train=True, download=True, transform=transform)
train_loader = torch.utils.data.DataLoader(train_dataset, batch_size=64, shuffle=True)
test_dataset = datasets.MNIST('data', train=False, download=True, transform=transform)
test_loader = torch.utils.data.DataLoader(test_dataset, batch_size=1000, shuffle=False)
test_plot_loader = torch.utils.data.DataLoader(test_dataset, batch_size=1, shuffle=True)
# 2. Model
class Net(nn.Module):
def __init__(self):
super(Net, self).__init__()
self.net = nn.Sequential(
nn.Linear(784, 512),
nn.Sigmoid(),
nn.Linear(512, 256),
nn.Sigmoid(),
nn.Linear(256, 128),
nn.Sigmoid(),
nn.Linear(128, 64),
nn.Sigmoid(),
nn.Linear(64, 10), # 10 classes
)
def forward(self, x):
return F.log_softmax(self.net(x), dim=1)
model = Net()
PATH = './mnist_model.pth'
model.load_state_dict(torch.load(PATH))
# x. Evaluate
correct = 0
fig, axes = plt.subplots(nrows=2, ncols=5, figsize=(16, 8))
axes = axes.flatten()
with torch.no_grad():
for data, target in test_loader:
output = model(data)
pred = output.argmax(dim=1, keepdim=True)
correct += pred.eq(target.view_as(pred)).sum().item()
for i in range(0,10):
images, labels = next(iter(test_plot_loader))
output = model(images)
pred = output.argmax(dim=1, keepdim=True)
img, lbl = images[0].squeeze(), labels.item()
axes[i].imshow(img.view(28,28), cmap="gray")
axes[i].set_title(f"true: {lbl} predicted: {pred.item()}")
plt.show()
print('\nTest set: Accuracy: {}/{} ({:.0f}%)\n'.format(
correct, len(test_loader.dataset),
100. * correct / len(test_loader.dataset)))MNIST Training
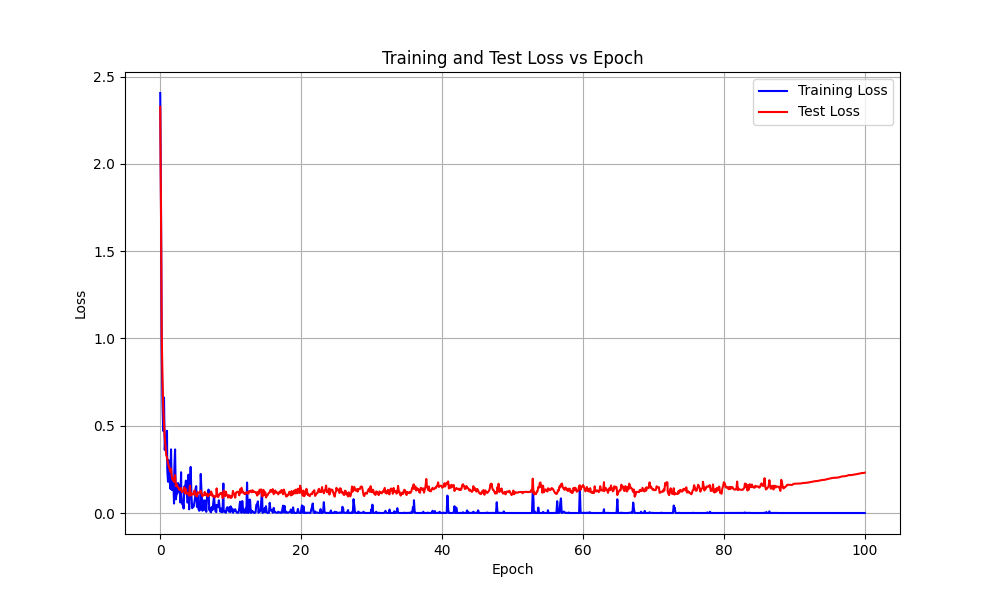
MNIST Training
## See `./code/mnist/mnist_mlp.py`
# 1. Data
# 2. Model
# 3. Loss and 4. Training
## Skips the plotting portion. See `mnist_mlp.py`
optimizer = optim.Adam(model.parameters())
for epoch in range(100):
for batch_idx, (data, target) in enumerate(train_loader):
optimizer.zero_grad()
output = model(data)
## Negative Log Likelihood loss defined within training loop:
loss = F.nll_loss(output, target)
loss.backward() # obtain gradients
optimizer.step() # update parameters "descent step"
if batch_idx % 100 == 0:
print('Train Epoch: {} [{}/{} ({:.0f}%)]\tLoss: {:.6f}'.format(
epoch, batch_idx * len(data), len(train_loader.dataset),
100. * batch_idx / len(train_loader), loss.item()))
# 5. Evaluate
# 6. Save model
PATH = './mnist_model.pth'
torch.save(model.state_dict(), PATH)CNNs and MNIST
## See `./code/mnist/mnist_cnn.py`
# 1. Data
# 2. Model
class Net(nn.Module):
def __init__(self):
super(Net, self).__init__()
self.conv1 = nn.Conv2d(1, 32, 3, padding=1)
self.conv2 = nn.Conv2d(32, 64, 3, padding=1)
self.pool = nn.MaxPool2d(2, 2)
self.fc1 = nn.Linear(7 * 7 * 64, 128)
self.fc2 = nn.Linear(128, 10)
def forward(self, x):
x = self.pool(F.relu(self.conv1(x)))
x = self.pool(F.relu(self.conv2(x)))
x = x.view(-1, 7 * 7 * 64)
x = F.relu(self.fc1(x))
x = self.fc2(x)
return F.log_softmax(x, dim=1)
model = Net()
# 3. Loss and 4. Training
# 5. Evaluate
# 6. Save modelDL Course • Home