0.22482872009277344 msec elapsed for NM
0.33402442932128906 msec elapsed for GNM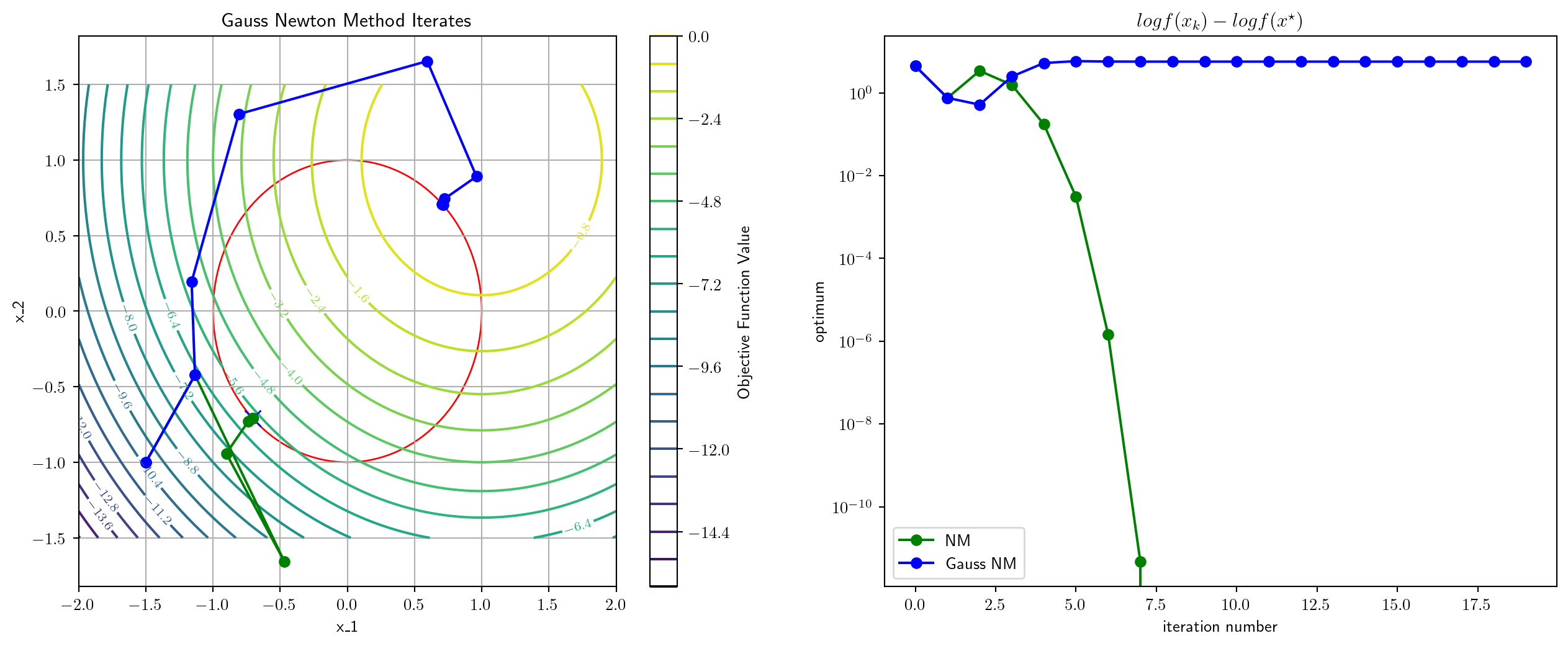
Instructor: Hasan A. Poonawala
Mechanical and Aerospace Engineering
University of Kentucky, Lexington, KY, USA
Topics:
Equality Constraints
Inequality Constraints
KKT Conditions
General nonlinear programming problems are of the form
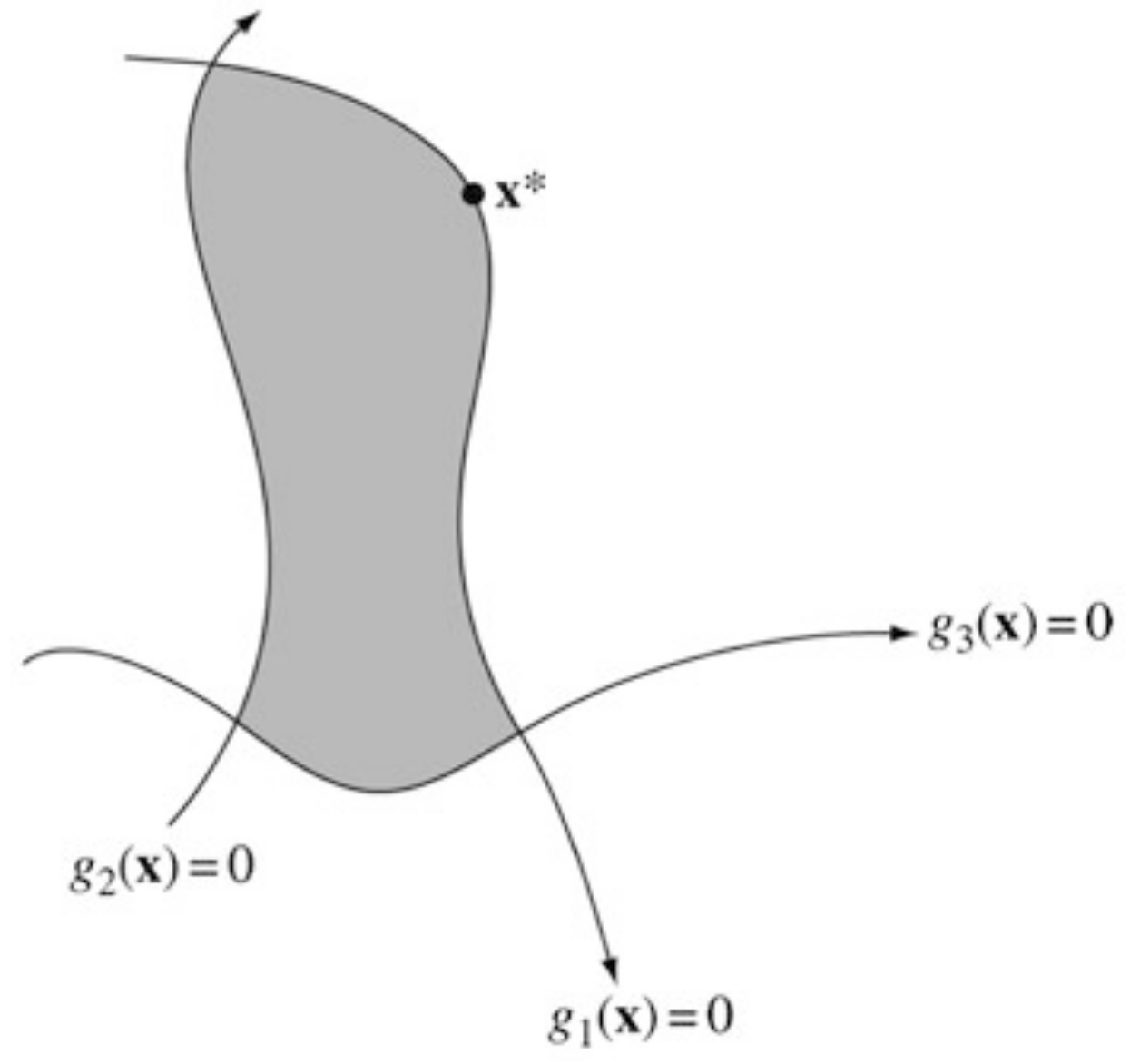
Definition
Consider all differentiable curves on passing through a point . The tangent plane at of is defined as the collection of the derivatives at of all these differentiable curves.
If is a regular point (to be defined) then we can make the following identification:
Another way: the tangent plane to is the set of all directions that are neither strict increase or strict decrease directions for
Definition (Regular Point)
A point satisfying the constraint is said to be a regular point of the constraint if the gradient vectors are linearly independent.
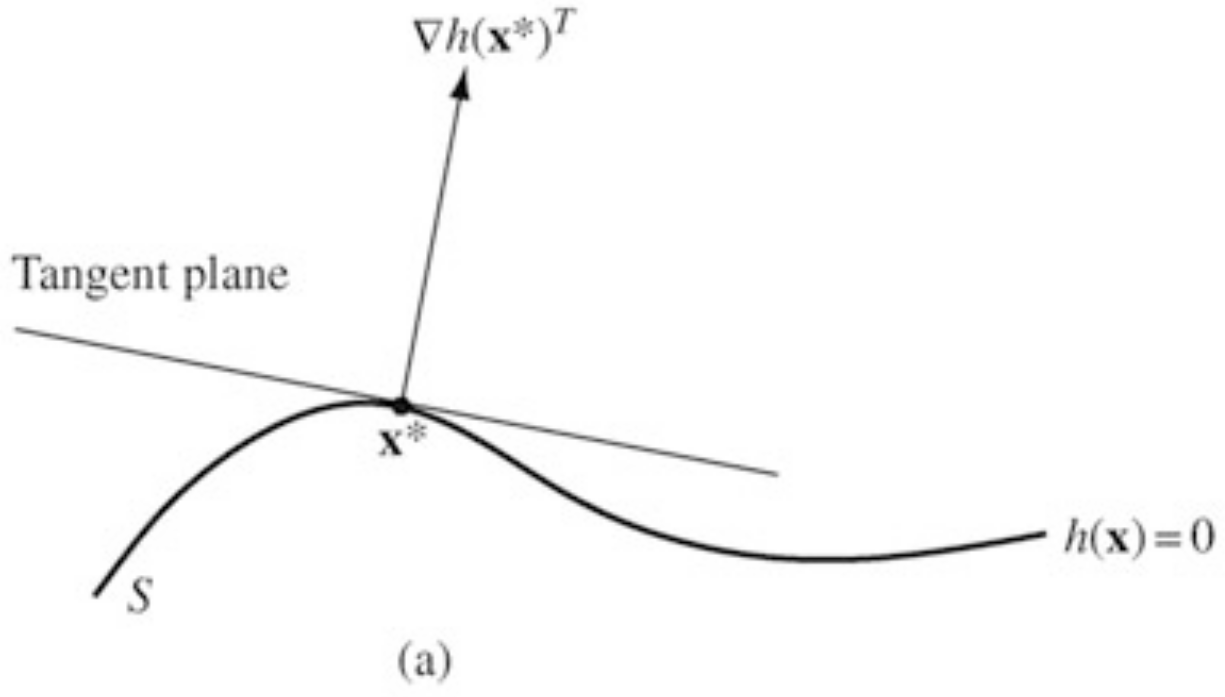
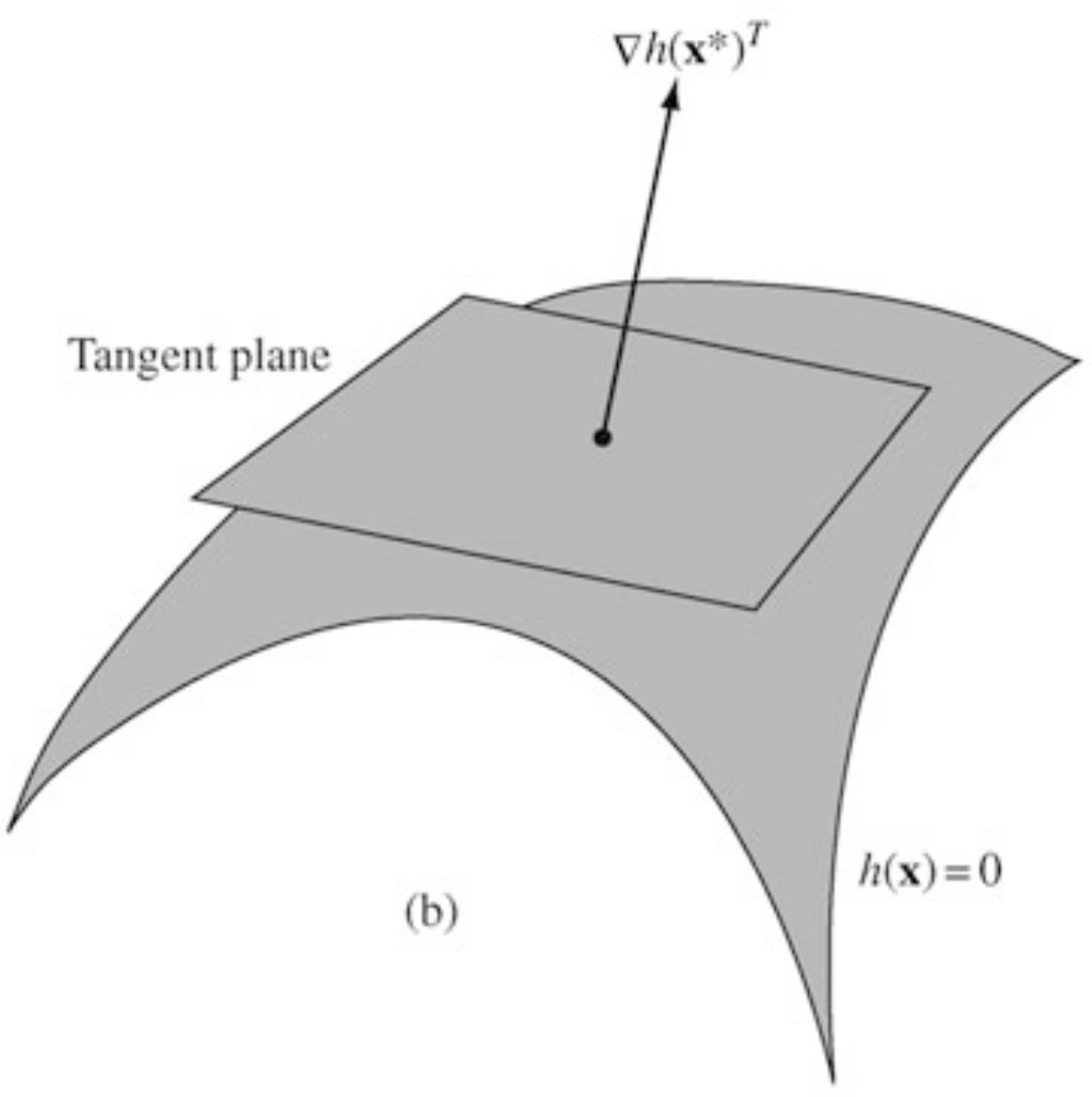
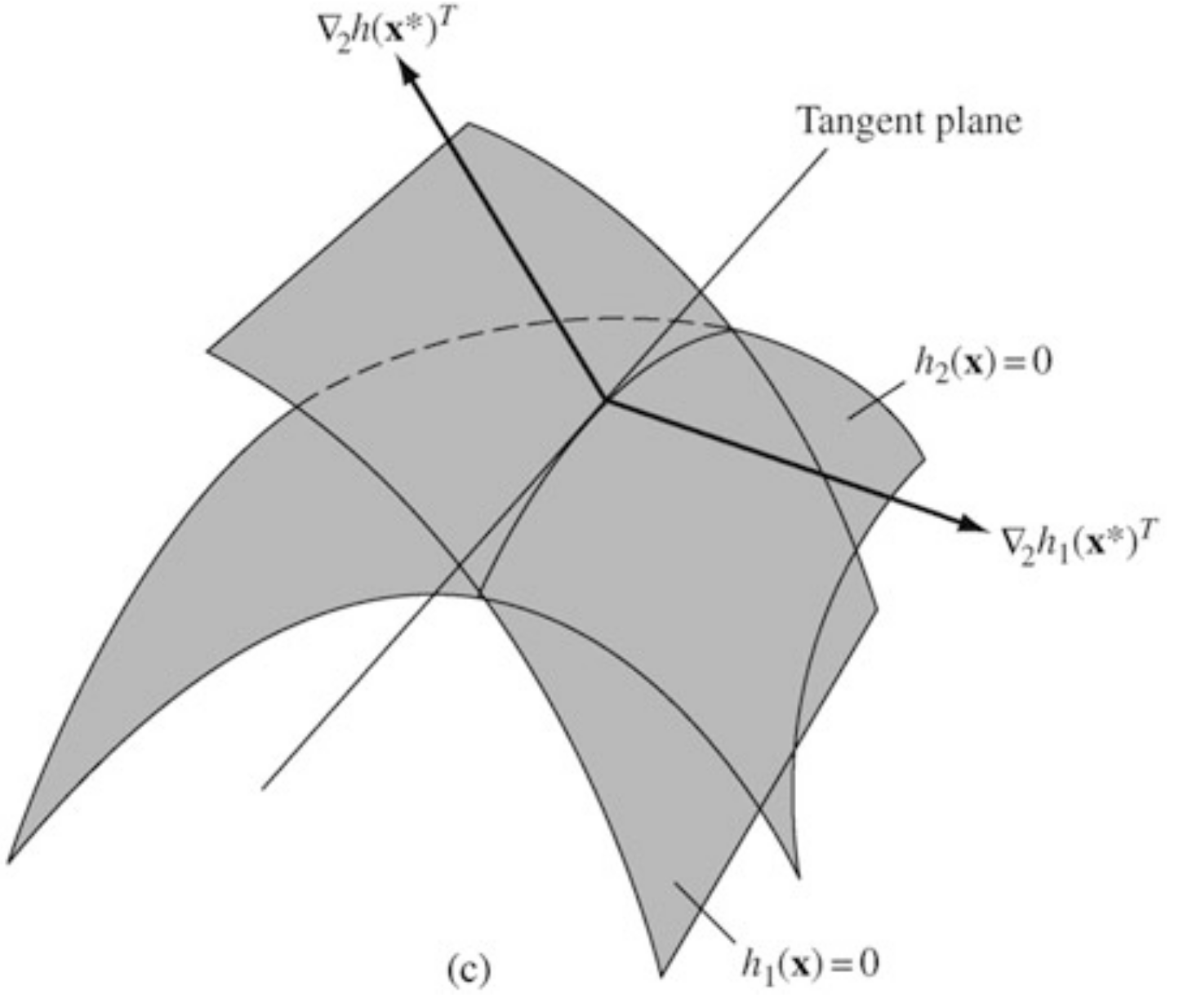
Lemma
Let be a regular point of the constraints and a local extremum point of subject to these constraints. Then for all , we have
Proof
Let and let such that and for for some .
Since is a constrained local minimum point of , we have
This lemma says that .
Theorem (FONC)
Let be a regular local minimum point of subject to the constraint . Then there is a such that
Proof
From the lemma, we may conclude that the linear system
has no feasible solution . Then, by Farkas’s lemma, its alternative system must have a solution. Specifically, there is a such that .
The FONC Equation 1 together with the constraints give a total of equations in the variables comprising .
Theorem
The first-order necessary conditions are sufficient if is convex and is affine.
The statements of various conditions often require that be a regular point1.
This requirement is known as a constraint qualification.
To see why constraint qualifications are important, consider the problem
The only feasible point is , so that is the (global) minimizer.
However, , and . cannot satisfy the FONC!
The Lagrange multipliers associated with a constrained minimization problem have an interpretation as prices, similar to the prices in LP.
Let a minimal solution be a regular point and be the corresponding Lagrange multiplier vector. Consider the family of problems
Sensitivity Theorem
Consider the family of problems Equation 4. Suppose that for every in a region containing , its minimizer is continuously differentiable depending on . Let with the corresponding Lagrange multiplier . Then
Sensitivity Theorem
Consider the family of problems Equation 4. Suppose that for every in a region containing , its minimizer is continuously differentiable depending on . Let with the corresponding Lagrange multiplier . Then
Proof
Using the chain rule and taking derivatives with respect to on both sides of
at , we have
On the other hand, using the chain rule and the first-order condition for and the above matrix equality
Theorem (Farkas’s Lemma).
Let be an matrix and be an -vector. The system of constraints has a feasible solution if and only if the system of constraints has no feasible solution . Therefore a single feasible solution for system Equation 6 establishes an infeasibility certificate for the system Equation 5.
Example 1
Suppose . Then, is feasible for system Equation 6, which proves that the system Equation 5 is infeasible.
Lemma
Let be the cone generated by the columns of matrix , that is Then C is a closed and convex set.
Proof (of Farkas’s Lemma).
Let the system Equation 5 have a feasible solution, say . Then, the system Equation 6 must be infeasible, since, otherwise, we have a contradiction
from and .
Now, let the system Equation 5 have no feasible solution, that is, . We now prove that its alternative system Equation 6 must have a feasible solution.
Since points is not in and is a closed convex set, by the separating hyperplane theorem, there is a such that But we know that for some , so we have Setting , we have from inequality Equation 7.
Proof (of Farkas’s Lemma) - Continued -
Furthermore, inequality Equation 7 also implies . Since otherwise, say the first entry of , , is positive. We can then choose a vector such that
Then, from this choice, we have
This tends to as . This is a contradiction because should be bounded from above by inequality Equation 7. Therefore, identified in the separating hyperplane theorem is a feasible solution to system Equation 6. Finally, we can always scale such that .
Geometric Interpretation
If is not in the closed and convex cone generated by the columns of the matrix , then there must be a hyperplane separating and the cone, and the feasible solution to the alternative system is the slope-vector of the hyperplane.
Corollary
Let be an matrix and an -vector. The system of constraints
has a feasible solution if and only if the system of constraints
has no feasible solution . Therefore a single feasible solution for system Equation 9 establishes an infeasibility certificate for the system Equation 8.
Theorem (SONC)
Suppose that is a regular local minimum of subject to . Then there is a such that If we denote by , the tangent plane, then the matrix on , that is, , .
Proof
From elementary calculus for every twice differentiable curve through we have Furthermore, differentiating the relation twice, we obtain Additing these two equations yields the result Since is arbitrary in , we have the stated conclusion.
Theorem (SOSC)
Suppose there is a point satisfying , and a such that Equation 10 holds. Suppose also that the matrix on . Then is a strict local minimum of subject to .
Proof
If is not a strict relative minimum point, a sequence of feasible points converging to s.t. for each , . Write , where and , . By Bolzano-Weierstrass some subsequence of converges. WLOG assume . We also have which implies . We have
Multiply Equation 12 by and add to Equation 13 to obtain
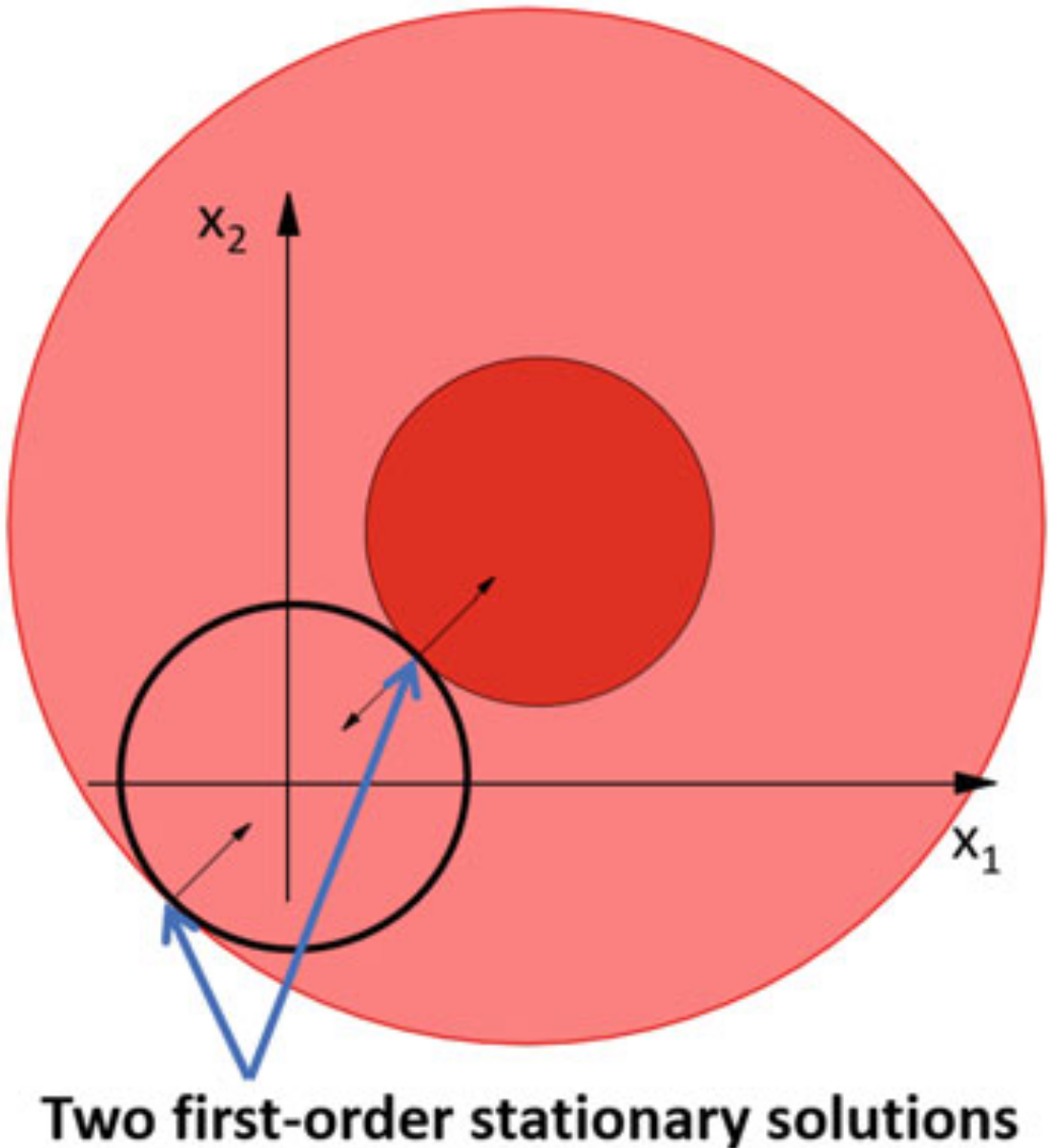
Consider the problem
The Lagrangian and subsection FONC would be
From the two equations we conclude , together with .
We have the two first-order stationary solutions
The Lagrangian Hessian matrix at these s becomes
Problem
FONC
with one solution , , , .
SOC
and the corresponding subspace is
In this case is the subspace spanned by the standard bases and of .
Therefore the restriction of is computed to be
Alternatively, we can construct matrices and determinants of order rather than .
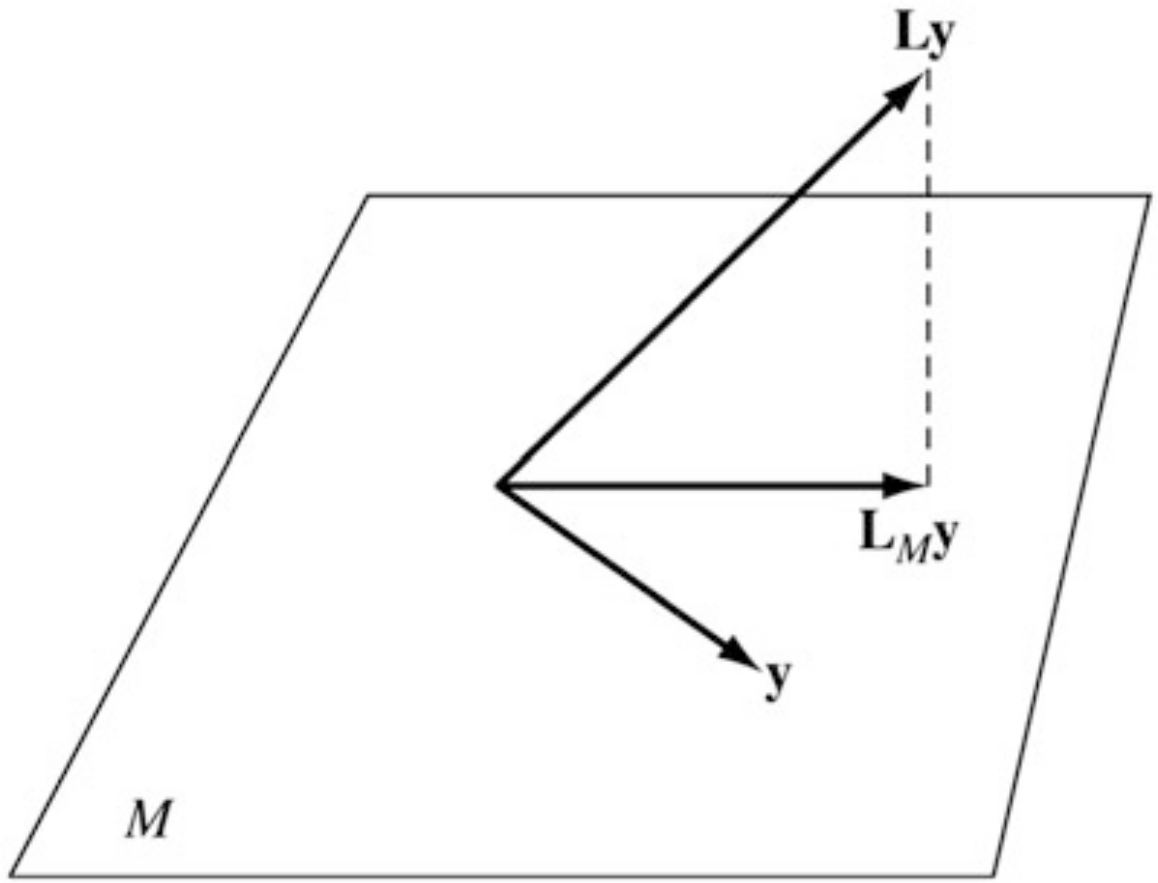
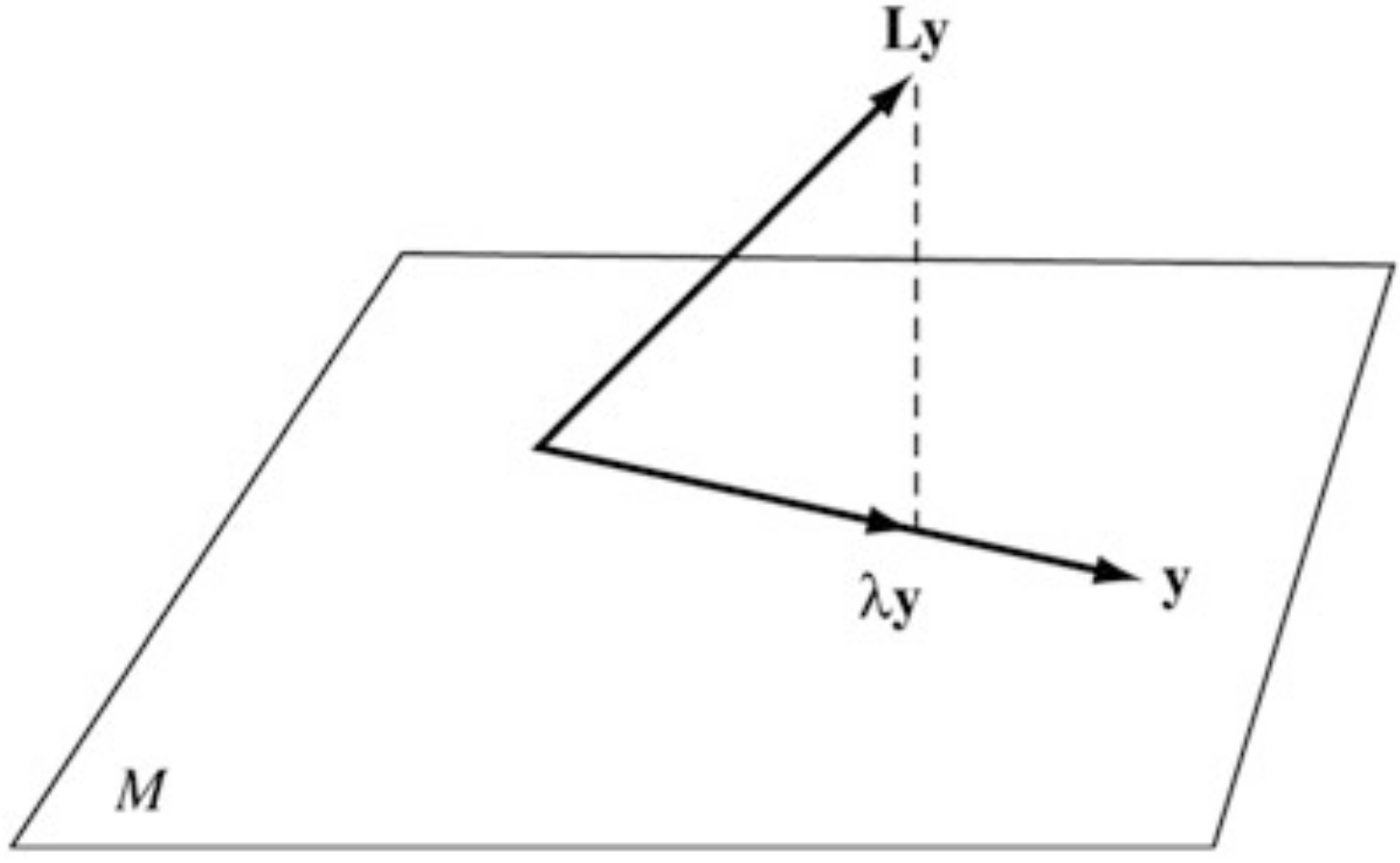
For simplicity, let , which has full row rank.
Any satisfying can be expressed as
is the so-called projection matrix onto the nullspace of (i.e. onto )
Projected Hessian Test
The matrix is positive definite on iff the projected Hessian matrix to is positive semidefinite with rank .
In the previous example we had . Hence
Definition (relative minimum or local minimum).
A point is said to be a relative minimum point of over if such that for all within a distance of .
Definition (global minimum).
A point is said to be a global minimum point of over if for all .
Feasible direction
Given we say that a vector is a feasible direction at if there is an such that for all with .
Descent direction
An element of the set of directions with the property is called a descent direction.
If , then there is such that for all with . The direction is the steepest descent one.
Consider the variable , and the inequality constrained optimization problem
The feasible region is
Definition
Let be a point satisfying the constraints
and let be the set of indices for which . Then is said to be a regular point of the constraints Equation 14 if the gradient vectors , , , are linearly independent.
Karush-Kuhn-Tucker (KKT) Conditions
Let be a relative minimum point for the problem
and suppose is a regular point for the constraints. Then there is a vector and a vector with such that
We can combine all the conditions into:
Proof
Since and , the second of Equation 16 is equivalent to the statement that a component of may be nonzero only if the corresponding constraint is active. This is a complementary slackness condition studied in LP, which states that implies and implies .
Since is a relative minimum point over the constraint set, it is also a relative minimum over the subset of that set defined by setting the active constraints to zero. Thus, for the resulting equality constrained problem, defined in a nbhd. of , there are Lagrange multipliers. Therefore, we conclude that first of Equation 16 holds with if .
It remains to be shown that . Suppose for some . Let and be the surface and the tangent plane, resp., defined by all other active constraints at . By the regularity assumption, there is a such that , that is, and for all but , and . Multiplying this from the right to the first of Equation 16, we have
which implies that is a descent direction for the objective function.
Let with and . Then for small , is feasible – it remains on the surface of and because (that is, constrant becomes inactive). But
which contradicts the minimality of .
Example 1
Example 2
Example 3
Example 4
The Lagrangian Derivative Constraint for Examples 1 & 2 is going to be of the form
If , then . Thus, if is feasible, it is a local minimizer.
If , then (Example 1) or (Example 2), and is a local minimizer.
.
The Lagrangian Derivative Constraint for Examples 3 & 4 is going to be of the form
If , then . Thus, if is feasible, it is a local minimizer.
If , then (Example 3) or (Example 4)
.
Example 5
Example 6
Example 7
Introduce the Lagrangian associated with the problem, defined as
The first KKT condition becomes
If is convex and is affine , and are concave functions, then is convex in for every fixed and .
Therefore if meets the first of Equation 16, then is the global minimizer of for given and (FOSC-UCO).
Theorem
The FONC are sufficient if is convex, is affine, and is concave for all .
Proof
Let be any feasible solution and , together with and satisfy the FONC. Then we have
which completes the proof.
Same as equality constrained optimization once you identify the active constraints
SONC
Suppose is a regular point of the constraints. If is a relative minimum point for the problem Equation 15, then there is a , , such that Equation 16 hold and such that is positive semidefinite on the tangent subspace of the active constraints in .
SOSC
Sufficient conditions that a point satisfying Equation 14 be a strict relative point of the problem Equation 15 is that there exist , such that
and the Hessian matrix
is positive definite on the subspace
where .
Maximal flow problem
Determine the maximal flow that can be established in such a network.
where for those no-arc pairs .

-dimensional data points are to be classified into two distinct classes.
where is the desired hyperplane.
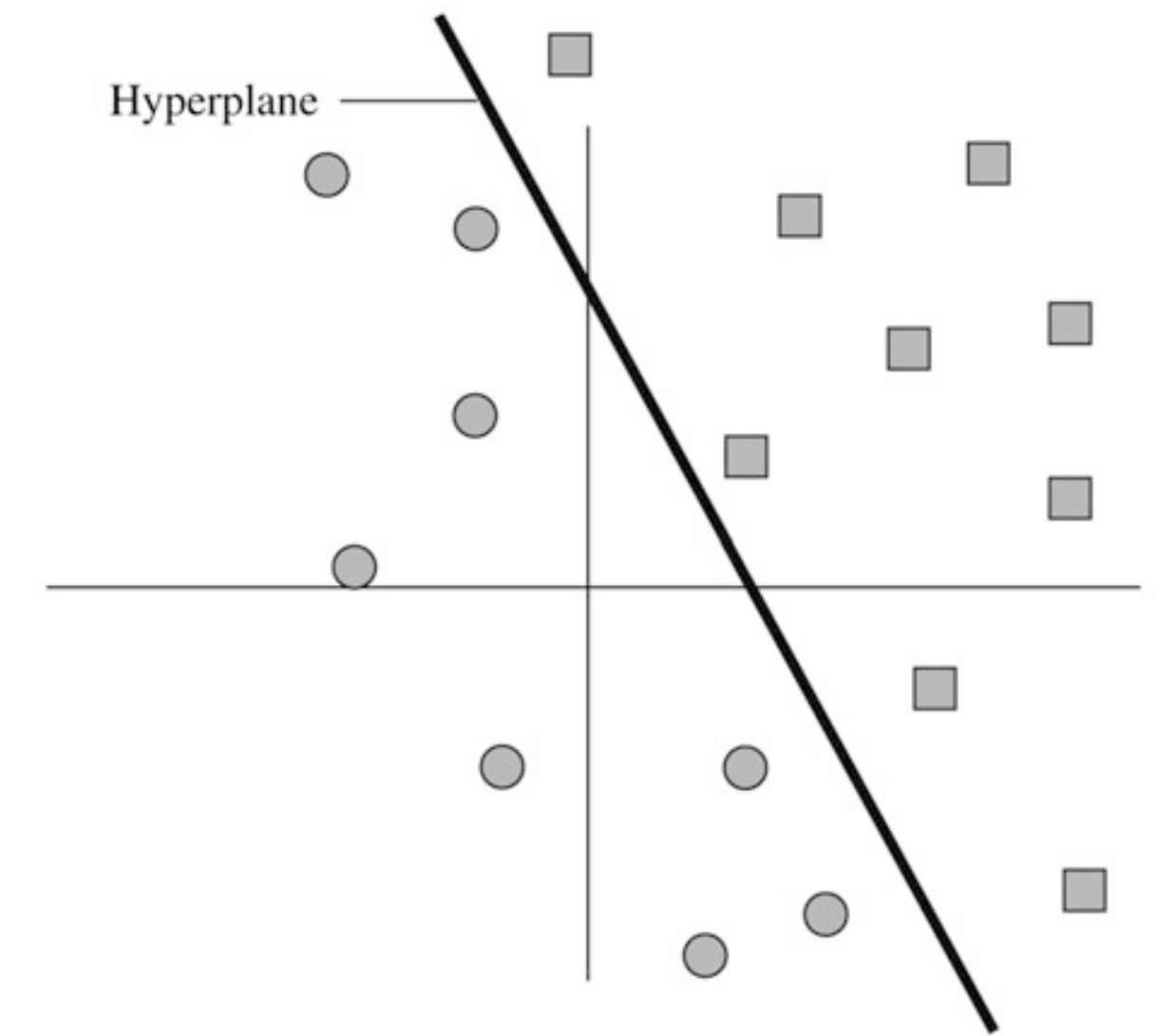
Example
Optimization problem
Lagrangian
First-Order Conditions
(MSC): .
(LDC):
(CSC):
Consider the problem

fmincon% Define the objective function
fobj = @(x) -(x(1) - 1)^2 - (x(2) - 1)^2;
% Define the equality constraint
hcon = @(x) x(1)^2 + x(2)^2 - 1;
% Convert equality constraint to the required function handle format
nonlcon = @(x) deal(hcon(x),[]); % Equality constraints in first output, inequality constraints in second
% Initial guess
x0 = [2; 1.0];
% Set optimization options
options = optimoptions('fmincon', 'Algorithm', 'sqp', 'Display', 'iter');
% Solve the optimization problem
tic
[x_opt, fval, exitflag, output] = fmincon(fobj, x0, [], [], [], [], [], [], nonlcon, options);
toc
% Display results
disp('Optimal solution:')
disp(x_opt)
disp('Optimal function value:')
disp(fval)0.22482872009277344 msec elapsed for NM
0.33402442932128906 msec elapsed for GNM
Generally: . Solve for given .
0.23674964904785156 msec elapsed for NM
2.579927444458008 msec elapsed for GNM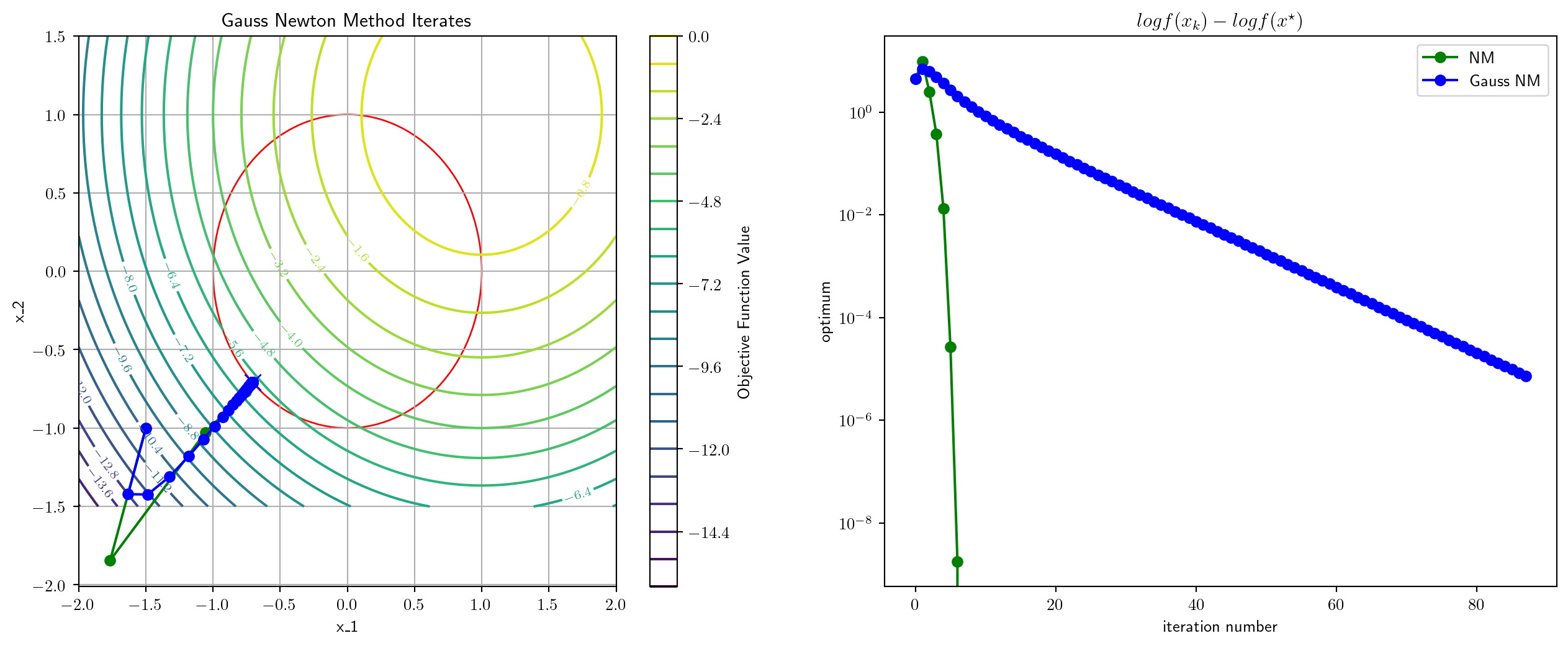
0.2040863037109375 msec elapsed for NM
0.2949237823486328 msec elapsed for GNM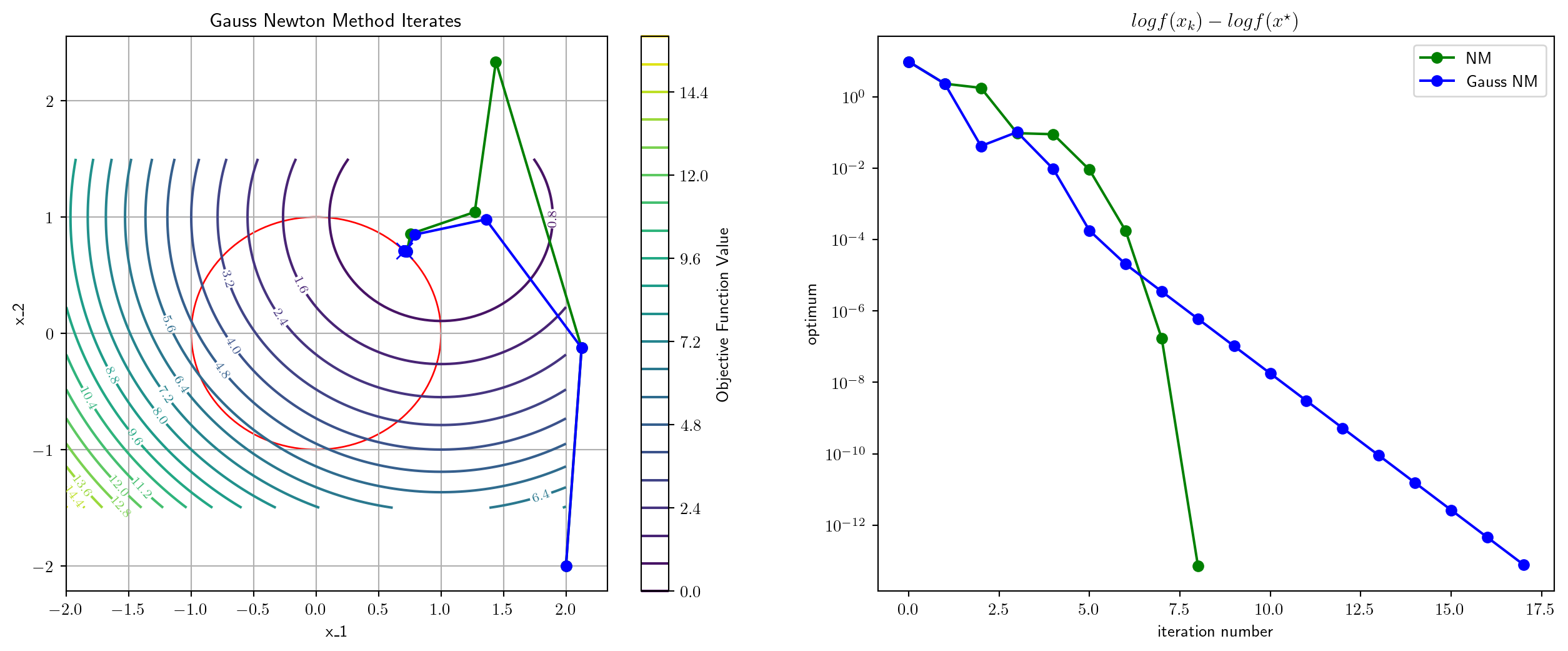
cvx:cvx_begin
variables x1 x2 % Define optimization variables
% Define the objective function
minimize( (x1 - 1)^2 + (x2 - 1)^2 )
% Define the inequality constraint
subject to
x1^2 + x2^2 <= 1 % Constraint: x1^2 + x2^2 ≤ 1
cvx_end
% Display results
disp('Optimal solution:')
disp([x1, x2])
disp('Optimal function value:')
disp(cvx_optval)cvxpy:# Import packages.
import cvxpy as cp
import numpy as np
import time
# Define and solve the CVXPY problem.
w = cp.Variable(2)
prob = cp.Problem(cp.Minimize( cp.norm(w - np.array([1.0,1.0] ) ) ),[cp.norm(w)<=1] )
# Solve the problem, and time it
tic=time.time()
prob.solve()
toc=time.time()
# Print result.
print("\nThe optimal value is", prob.value)
print("The solution x is x=", w.value)
print("time taken:",1000*(toc-tic), "msec")
The optimal value is 0.4142135615262684
The solution x is x= [0.70710678 0.70710678]
time taken: 1.7130374908447266 msec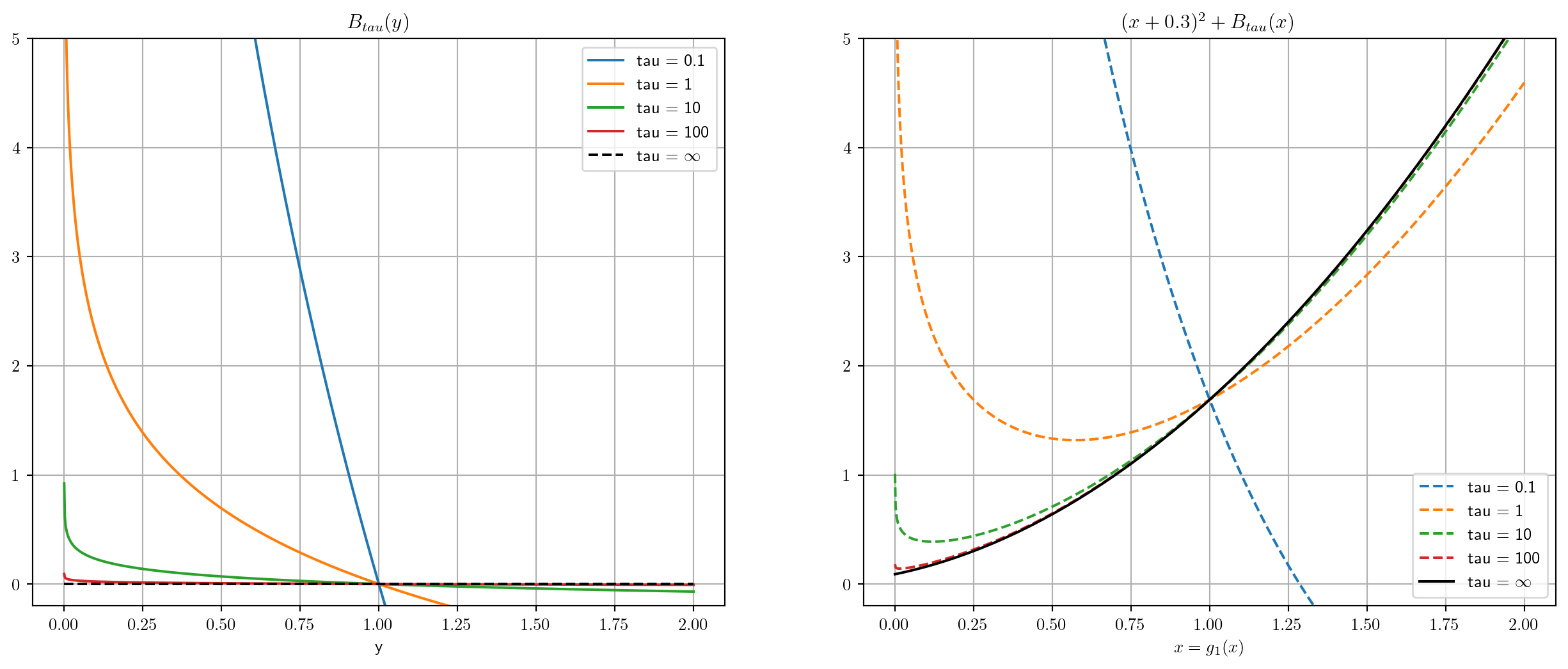
3.275632858276367 msec elapsed for NM[0.70710678 0.70710678]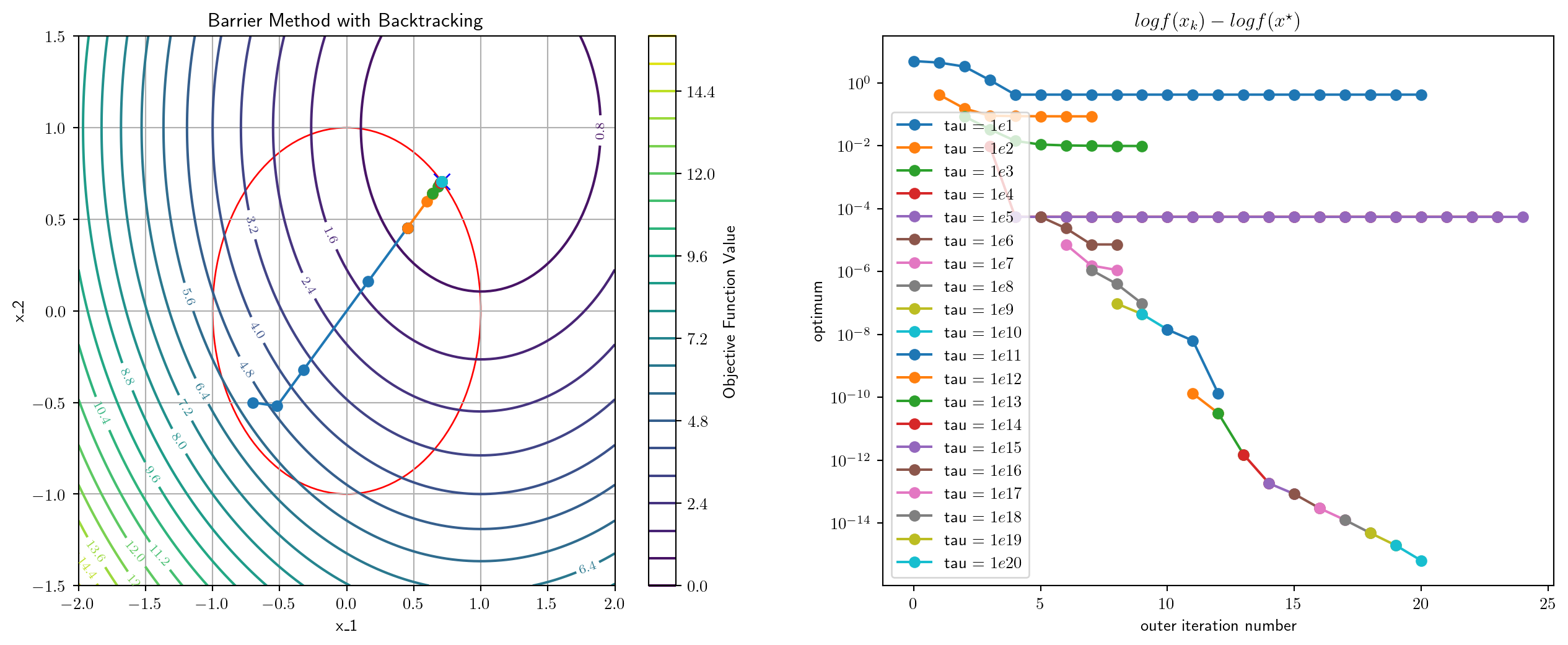
If for , then we satisfy OVC and also MSC.
What about CSC?
0.4711151123046875 msec elapsed for PD-IP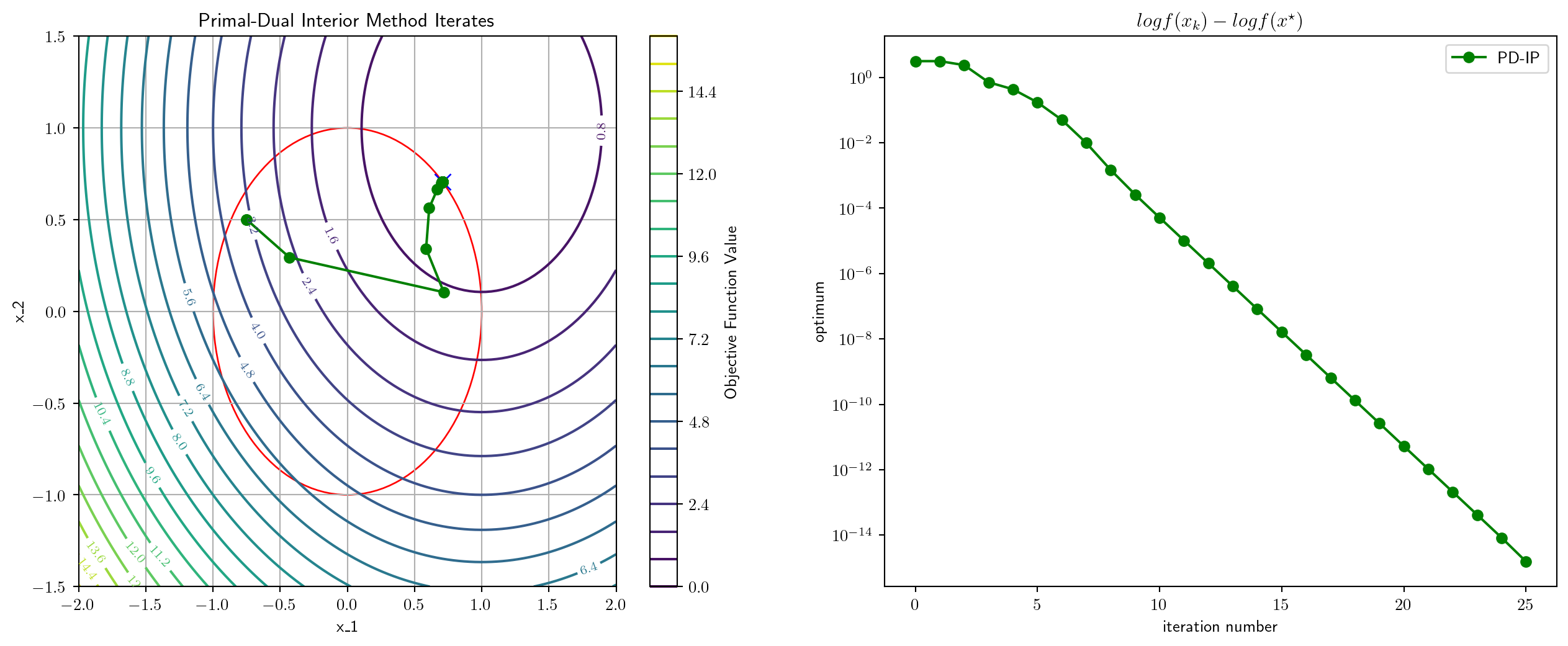
becomes
For any , we can choose , producing a strictly feasible point for the second problem.
For equality constraints, first solve
If , we have a strictly feasible point for the original problem
is equivalent to
which becomes
becomes
Systems Optimization I • ME 647 Home