ME/AER 647 Systems Optimization I

---

Mixed Integer Linear Programming

Instructor: Hasan A. Poonawala

Mechanical and Aerospace Engineering
University of Kentucky, Lexington, KY, USA

Topics:
Examples
Branch n Bound

Traveling Salesman Problem

Consider $n$ locations $p_i$ with distance $c_{i j}$ between locations $p_i$ and $p_j$.

Traveling Salesman Problem (TSP)

The TSP involves finding the shortest path (sequence of locations) that visits each location exactly once and returns to the start location.

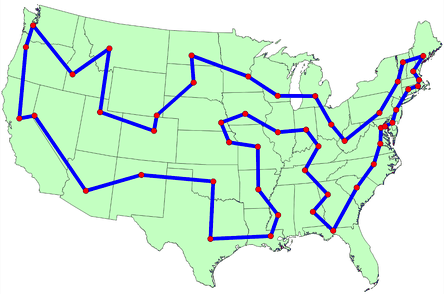
48 States TSP

Find a closed route that visits all state capitols in the contiguous USA once.

48 States TSP Solution

Available from: https://optimization.cbe.cornell.edu/index.php?title=File:48StatesTSP.png

TSP Formulation

• Variables: $$\begin{align} x_{ij}={\begin{cases}1&{\text{the path goes from city }}i{\text{ to city }}j\\0&{\text{otherwise.}}\end{cases}} \end{align}$$
• Optimization problem: $$\begin{aligned} \min_{x_{ij}} &\sum _{i=1}^{n}\sum _{j\neq i,j=1}^{n}c_{ij}x_{ij}\colon &&\\ \text{subject to } &\sum _{i=1,i\neq j}^{n}x_{ij}=1&&j=1,\ldots ,n;\\ &\sum _{j=1,j\neq i}^{n}x_{ij}=1&&i=1,\ldots ,n;\\ &\sum _{i\in Q}{\sum _{j\neq i,j\in Q}{x_{ij}}}\leq |Q|-1&&\forall Q\subsetneq \{1,\ldots ,n\},|Q|\geq 2.\\ & x_{ij} \in \{0,1\} && \forall i,j =1,\ldots ,n; \end{aligned}$$

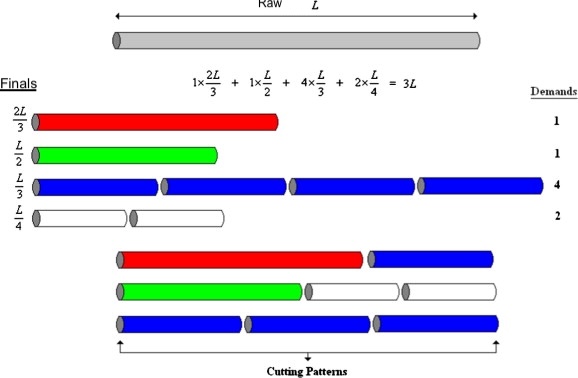
Cutting Stock

• A supplier produces rolls, called raws of some large length
• The supplier can cut these raws into finals of appropriate length according to manufacturer requirements.
• The manufacturer needs some combination of finals to produce components.

Available from: https://www.researchgate.net/figure/One-dimensional-cutting-stock-problem-with-one-stock-type_fig2_257451021

Patterns

A pattern is a combination of finals that can be cut from a single raw

Cutting Stock Problem

Find the smallest number of raws that the manufacturer must order and the corresponding patterns.

• The decision variables $x_i$ turn out to be the number of each type of pattern that must be ordered.

• There are as many variables as the number of patterns, and as many constraints as the number of patterns

  • The parameter $a_{ij}$ is the number of finals of type $j$ produced from pattern $i$

MILP Formulation

• Optimization problem:

$$\begin{align} \text{minimize }_{x_i} & \sum_{i=1}^n c_i x_i \\ \text{subject to } & \sum_{i=}^n a_{ij} x_i = q_j && j \in 1,\dots,m\\ & x_i \in \{0,1,2,\dots\} \end{align}$$

• $c_i$ is often unity
• $q_j$ are the number of finals of type $j$ required

Knapsack Problem

$$\begin{align} \text{maximize } & \sum v_i x_i \\ \text{subject to } & \sum w_i x_i \leq W\\ & x_i \in \{0,1,2,\dots\} \end{align}$$

• $x_i$: number of objects type $i$

• $w_i$: weight (or volume) object type $i$

• $v_i$: value of object type $i$

• $W$: Weight or volume limit of knapsack

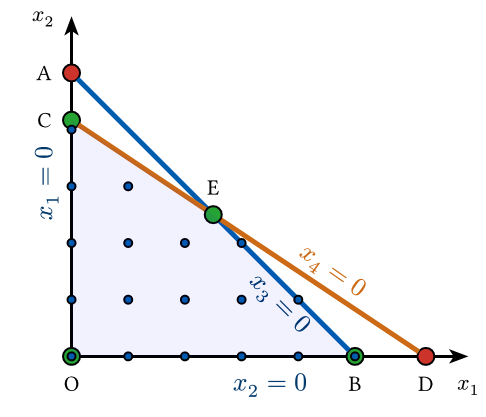
Linear Programming Relaxation

We can remove or relax the integrality constraints to obtain a linear program:

$$x_i \in \{0,1\} \rightarrow 0 \leq x_i \leq 1$$

$$x_i \in \{0,1,2,\dots\} \rightarrow x_i \geq 0$$

If we solve the resulting LP, solution may or may not be integer-valued

How does the solution of this relaxed linear program (RLP) relate to the original problem? Note: Consider maximization case

1. The optimal solution of the RLP is a upper bound for the optimal value of the MILP
2. If the optimal solution of the RLP is integer valued, the optimal value is an lower bound for the MILP optimal value

These conclusions lead to the Branch-and-Bound algorithm

Example:

Pattern	1	2	3	4	5	6	7	8	9	10
$2 L/3$	1	0	0	1	0	0	0	1	0	0
$L/2$	0	1	0	0	2	0	0	0	1	0
$L/3$	1	0	3	0	0	0	1	0	1	2
$L/4$	0	2	0	0	0	4	2	1	0	1

MILP Diagram

$$\begin{align} \text{min}_{x_1,x_2} & -5 x_1-7 x_2 \\ \text{subject to } & x_1+ x_2 \leq 5\\ & 4 x_1+ 6 x_2 \leq 25 \\ & x_i \in \{0,1,2,\dots\} \end{align}$$