Classification and Control
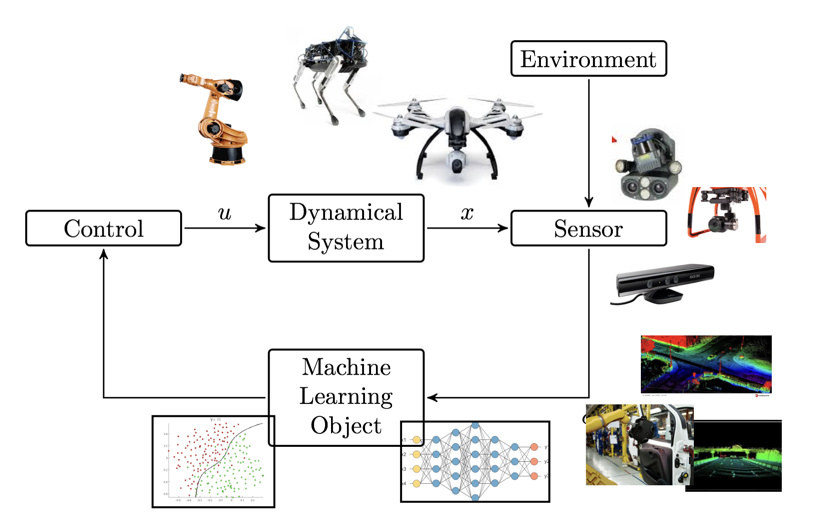
We develop models to analyze how the presence of learned classifiers in feedback loops affects the latter's performance. We work on the following projects in this area:
Classifier-in-the-Loop Systems as Hybrid Systems:
Controllers for regulation and tracking tasks are usually functions of the state or measurement. A measurement is traditionally a unique value attached to each state of the system, perhaps corrupted by noise. The output of sensors like optical cameras and LIDAR, however, can be rich and complex, and the state may be difficult to extract from them. The richness often comes from the influence of an unknown environment on the measurement. A known mapping from state to measurement is absent for such sensors precluding estimation of the state by traditional methods.
Knowledge of the state is unnecessary in some control scenarios. Measurement-based feedback is sufficient to control the plant, but only when the mapping from state to measurement is known. Machine Learning techniques can extract such a map from complex measurements. This map is unreliable when the measurement includes features due to an unknown environment. Accurately differentiating between the environment and the state is impossible. A classifier can be used to coarsely identify the appropriate control from such measurements. Each element of the training data consists of a state, the measurement in that state, and the correct control decision (represented by a class label).
The class labels define disjoint subsets of the measurement space, separated by decision surfaces. These decision surfaces induce switching surfaces in the state space across which the control abruptly changes from one finite value to another. This leads to the closed-loop system being a switched system. The switching surfaces can be estimated from the training data leading to a nominal closed-loop model.
The following questions arise:
Is the nominal switched system derived from data stable?
If the true switched system is different from the nominal switched system, will the conclusions related to stability of the nominal system hold for the true system?
If the environment in which the classifier is used is different from that in which the data was collected, will the closed-loop system still be stable?
These problems motivate establishing a notion of robustness for classifier-in-the-loop systems. We use the concept of structural stability of systems to answer the questions above.